(Page en perpétuelle construction...)
Soit κ le mot de Kolakoski (qui a été défini antérieurement par R. Oldenburger[1]), i.e. la séquence A000002 de l’OEIS.
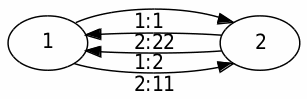
Soit T le transducteur suivant.

κ est un point fixe de T. L’autre point fixe est κ′, avec κ = 1κ′. Les transducteurs peuvent aisément se composer. Voici par exemple T2 et T3.
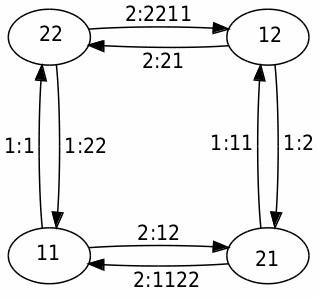
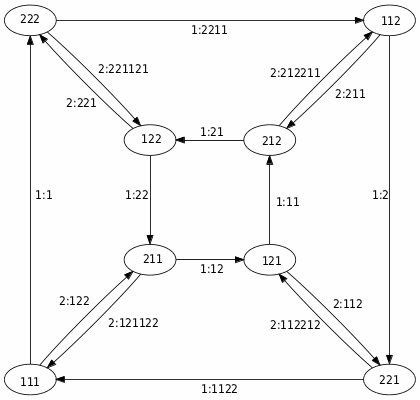
κ est également un point fixe de Tn pour tout n > 0. Plus généralement, tout mot infini lisse est l’image d’un mot infini lisse par Tn. On peut noter que Tn, pour n > 1, a d’autres points fixes que κ et κ′.
On peut émettre beaucoup de conjectures sur les transducteurs Tn.
Un chemin (fini ou non) dans un transducteur est valide s’il est induit par un mot lisse (fini ou non).
Conjecture. Soit n > 0.
Dans le cas du mot de Kolakoski sur l’alphabet {a,b}, avec a et b impair, ces conjectures sont trivialement fausses: Tn est une union de 2n-1 composante connexe de taille 2. Ceci peut expliquer pourquoi l’analyse est plus simple dans ces cas. Quand a et b sont pair, tous les cycles (et plus généralement, tous les arcs) dans T2 sont de poids 1∕2, ce qui donne directement la limite de 1∕2 pour les fréquences de a et b.
Observation. Le mot de Kolakoski est un chemin infini commençant à l’état o = 1…1. La post étiquette un de l’arc pré étiquette 2 partant du sommet o dans Tn est un préfixe du mot de Kolakoski, et la suite des un converge vers κ. L’arc pré étiquette 1 depuis o va à l’état o′ = 2…2, et les arcs partant de o′ sont post étiquetté par des préfixes de κ′. Il existe donc une fonction a : ℕ → ℝ, convergeant vers 0, telle que pour tout chemin infini w partant de o dans Tn, on a dist(w′,κ) ≤ a(n), où w′ est le chemin transduit par w.
Tout mot infini lisse (dont κ) est un chemin infini dans Tn. Le “cycles moyen maximum” (mean cycle) de Tn est donc d’une borne supérieure pour la densité du nombre de 1 dans κ, et dans tout mot lisse infini. Le tableau suivant donne les cycles moyens maximums dans Tn. (On peut noter qu’il y a une involution η entre les sommets de Tn telle que (x,w,y) ∈ E ssi (η(x),w,η(y)) ∈ E pour tout x,y ∈ V (Tn) et w ∈{1,2}*. Ceci explique que la borne obtenue est une borne supérieure pour la densité de 1 et de 2.)
| n | nbr. arcs | cycle moyen max. | fraction réduite | forme décimale |
| 1 | 2 | 2/3 | 2/3 | 0.666666666666666666666666666666 |
| 2 | 2 | 2/3 | 2/3 | 0.666666666666666666666666666666 |
| 3 | 2 | 5/9 | 5/9 | 0.555555555555555555555555555555 |
| 4 | 4 | 8/15 | 8/15 | 0.533333333333333333333333333333 |
| 5 | 8 | 36/69 | 12/23 | 0.521739130434782608695652173913 |
| 6 | 8 | 36/69 | 12/23 | 0.521739130434782608695652173913 |
| 7 | 8 | 64/123 | 64/123 | 0.520325203252032520325203252032 |
| 8 | 8 | 64/123 | 64/123 | 0.520325203252032520325203252032 |
| 9 | 16 | 286/561 | 26/51 | 0.509803921568627450980392156862 |
| 10 | 16 | 286/561 | 26/51 | 0.509803921568627450980392156862 |
| 11 | 16 | 624/1234 | 312/617 | 0.505672609400324149108589951377 |
| 12 | 16 | 1158/2295 | 386/765 | 0.504575163398692810457516339869 |
| 13 | 22 | 1992/3952 | 249/494 | 0.504048582995951417004048582995 |
| 14 | 64 | 10333/20535 | 10333/20535 | 0.503189676162649135622108595081 |
| 15 | 24 | 5310/10557 | 590/1173 | 0.502983802216538789428815004262 |
| 16 | 32 | 9912/19737 | 3304/6579 | 0.502203982368141054871561027511 |
| 17 | 56 | 28157/56097 | 28157/56097 | 0.501934149776280371499367167584 |
| 18 | 44 | 30975/61761 | 1475/2941 | 0.501530091805508330499829989799 |
| 19 | 28 | 30354/60555 | 10118/20185 | 0.501263314342333415902898191726 |
| 20 | 194 | 284631/568101 | 94877/189367 | 0.501021825344436992717844186157 |
| 21 | 268 | 616904/1231743 | 10456/20877 | 0.500838243042582746563203525410 |
| 22 | 32 | 102011/203721 | 14573/29103 | 0.500738755454764113665257877194 |
| 23 | 186 | 923194/1844197 | 923194/1844197 | 0.500594025475586393427600196725 |
| 24 | 424 | 3087156/6168369 | 1029052/2056123 | 0.500481731880826195709108842223 |
| 25 | 186 | 2126206/4249033 | 2126206/4249033 | 0.500397619881982559325851317229 |
| 26 | 12 | 252577/504818 | 252577/504818 | 0.500332793204679706349615108811 |
| 27 | 390 | 9857581/19704826 | 9857581/19704826 | 0.500262270775697283497961362358 |
| 28 | 256 | 9698478/19388547 | 3232826/6462849 | 0.500216854826718061956886196784 |
| 29 | 728 | 42019230/84008607 | 14006410/28002869 | 0.500177678222899232217955953013 |
| 30 | 1652 | 147516178/294946897 | 147516178/294946897 | 0.500144871841116538344188784600 |
| 31 | 26 | 3688655/7375520 | 737731/1475104 | 0.500121347376185001193136212768 |
| 32 | 22 | 3845003/7688497 | 3845003/7688497 | 0.500098133614411243185761794535 |
| 33 | 1548 | 455920839/911696379 | 13815783/27627163 | 0.500079686068381324568143316054 |
La différence entre le cycle moyen maximum et 1∕2 semble être en O((2∕3)n∕2) = O(0.816497n). Voici les rapports entre les cycles moyen maximum de deux transducteurs successifs.
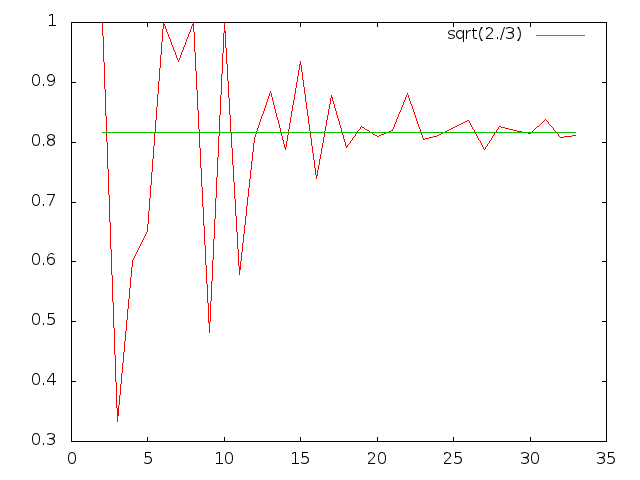
Remarque. Monter au dessus de T33 devient difficile, car les algorithmes efficaces et parallélisables pour calculer le cycle moyen maximum (algorithme d’Howard et variantes) manipulent un vecteur de valeurs (ici, des entiers 64 bits) de la taille le nombre de sommet du transducteur, c’est à dire 2n. Le stockage du transducteur est moins gênant, car il peut être calculé à la volée depuis d’un transducteur plus petit.
Il existe donc une constante c telle que pour tout i > c,
![|κ[1..i]|1
0.4999 < ---i--- < 0.5001.](kola0x.png)
Pour rappel, voici les bornes obtenues par V. Chvátal[3] par cycle moyen sur ses graphes (notés ici Cn).
| n | cycle moyen max. | fraction réduite | forme décimale |
| 1 | 1/1 | 1/1 | 1.000000000000000000000000000000 |
| 2 | 2/3 | 2/3 | 0.666666666666666666666666666666 |
| 3 | 2/3 | 2/3 | 0.666666666666666666666666666666 |
| 4 | 5/9 | 5/9 | 0.555555555555555555555555555555 |
| 5 | 8/15 | 8/15 | 0.533333333333333333333333333333 |
| 6 | 36/69 | 12/23 | 0.521739130434782608695652173913 |
| 7 | 36/69 | 12/23 | 0.521739130434782608695652173913 |
| 8 | 64/123 | 64/123 | 0.520325203252032520325203252032 |
| 9 | 64/123 | 64/123 | 0.520325203252032520325203252032 |
| 10 | 286/561 | 26/51 | 0.509803921568627450980392156862 |
| 11 | 286/561 | 26/51 | 0.509803921568627450980392156862 |
| 12 | 624/1234 | 312/617 | 0.505672609400324149108589951377 |
| 13 | 1158/2295 | 386/765 | 0.504575163398692810457516339869 |
| 14 | 1992/3952 | 249/494 | 0.504048582995951417004048582995 |
| 15 | 10333/20535 | 10333/20535 | 0.503189676162649135622108595081 |
| 16 | 5310/10557 | 590/1173 | 0.502983802216538789428815004262 |
| 17 | 9912/19737 | 3304/6579 | 0.502203982368141054871561027511 |
| 18 | 28157/56097 | 28157/56097 | 0.501934149776280371499367167584 |
| 19 | 30975/61761 | 1475/2941 | 0.501530091805508330499829989799 |
| 20 | 30354/60555 | 10118/20185 | 0.501263314342333415902898191726 |
| 21 | 284631/568101 | 94877/189367 | 0.501021825344436992717844186157 |
| 22 | 616904/1231743 | 10456/20877 | 0.500838243042582746563203525410 |
On voit que le cycle moyen maximum du graphe Cn+1 de Chvátal correspond au cycle moyen maximum de Tn. Cela vient du fait qu’il y a un morphisme de graphe ρ : V (Cn+1) → V (Tn); les sommets w1 et w2 sont envoyés sur le même sommet dans Tn.
Soit W un code sur {1,2} , et TW le transducteur à un état, et qui associe w à w pour tout w ∈ W. On note T * W le transducteur T * Tw.
Soit T un transducteur. Un mot est un mot de retour vers l’état v si le chemin partant de v et induit par w se termine sur v. Un mot est un mot de retour pour T s’il est un mot de retour pour tous les etats de T. L’ensemble des mots de retour lisses est naturelment un code préfixe maximal pour les mots lisses.
Le code suivant est l’ensemble des mots de retour dans T : W1 = {11,12,21,22}. T *W1 possède donc 2 composantes connexes d’un etat chacune, et pour tout n > 0, (Tn) * W1 a deux composantes connexes de taile 2n-1.
Pour T2, on a le code suivant (de taille 10) : W2 = {11, 121121, 12112212, 1212, 1221, 2112, 2121, 21221121, 212212, 22}. Pour T3, on a le code suivant (de taille 44) : W3 = {112112, 1121221121, 11212212, 11221211211221, 11221211212211, 1122121121221221, 11221221, 121121, 1211221211, 121122122112, 12112212212112112212, 12112212212112122112, 1211221221211221, 1212, 12211211212211, 12211211212212112212, 1221121121221221, 122112112212, 12211212212112112212, 1221121221211221, 1221121221221121, 12212112, 12212211, 1221221211211221, 1221221211212211, 12212212112212, 211211, 21121221, 2112212112112212, 2112212112122112, 21122121121221221121, 211221221121, 2112212212, 2121, 2122112112122112, 21221121121221211221, 21221121121221221121, 212211211221, 21221121221211211221, 212211212212112212, 21221121221221, 21221211, 2122122112, 22}. Pour tout n > 0, (Tn) * W2 a quatre composantes connexes de taile 2n-2, et (Tn) * W3 a huit composantes connexes de taile 2n-3.
Les avantages de multiplier par un code sont les suivants :
Le désavantage c’est que le nombre d’arcs partant d’un sommet est la taille du code. L’espace utilisé pour stocker le graphe devient beaucoup plus important, ou alors le temps pour calculer un arc explose, si on calcule les arcs à la volée.
Voici par exemple les cycles moyens maximums de Tn * W3 :
| n | nbr. arcs | cycle moyen max. | fraction réduite | forme décimale | gain par rapport à Tn |
| 4 | 1 | 22/42 | 11/21 | 0.523809523809523809523809523809 | 1.400000 |
| 5 | 2 | 36/69 | 12/23 | 0.521739130434782608695652173913 | 1.000000 |
| 6 | 2 | 64/123 | 64/123 | 0.520325203252032520325203252032 | 1.069565 |
| 7 | 2 | 64/123 | 64/123 | 0.520325203252032520325203252032 | 1.000000 |
| 8 | 4 | 286/561 | 26/51 | 0.509803921568627450980392156862 | 2.073171 |
| 9 | 4 | 286/561 | 26/51 | 0.509803921568627450980392156862 | 1.000000 |
| 10 | 4 | 369/729 | 41/81 | 0.506172839506172839506172839506 | 1.588235 |
| 11 | 8 | 1432/2835 | 1432/2835 | 0.505114638447971781305114638447 | 1.109093 |
| 12 | 6 | 1158/2295 | 386/765 | 0.504575163398692810457516339869 | 1.000000 |
| 13 | 7 | 2791/5545 | 2791/5545 | 0.503336339044183949504057709648 | 1.213481 |
| 14 | 12 | 9186/18267 | 3062/6089 | 0.502874035145344063064542617835 | 1.109825 |
| 15 | 14 | 15325/30507 | 15325/30507 | 0.502343724391123348739633526731 | 1.273103 |
| 16 | 3 | 5358/10669 | 114/227 | 0.502202643171806167400881057268 | 1.000608 |
| 17 | 4 | 10572/21076 | 2643/5269 | 0.501613209337635224900360599734 | 1.198945 |
| 18 | 30 | 121359/242103 | 40453/80701 | 0.501270120568518357888997658021 | 1.204682 |
| 19 | 18 | 102179/203919 | 102179/203919 | 0.501076407789367346838695756648 | 1.173639 |
| 20 | 14 | 99277/198213 | 99277/198213 | 0.500860185759763486754148315196 | 1.187912 |
| 21 | 6 | 71384/142533 | 71384/142533 | 0.500824370496656914539089193379 | 1.016828 |
| 22 | 3 | 59478/118808 | 29739/59404 | 0.500622853679886876304625951114 | 1.186082 |
| 23 | 21 | 607015/1212842 | 607015/1212842 | 0.500489758764950422231420086045 | 1.212894 |
| 24 | 56 | 2248103/4492659 | 2248103/4492659 | 0.500394755088245068232420933794 | 1.220331 |
| 25 | 124 | 7735770/15461487 | 859530/1717943 | 0.500325098096968292894467395018 | 1.223077 |
| 26 | 68 | 6417145/12827397 | 6417145/12827397 | 0.500268682726511076253428501511 | 1.238610 |
| 27 | 4 | 355310/710263 | 355310/710263 | 0.500251315357832239607018808525 | 1.043592 |
| 28 | 38 | 8517434/17028705 | 8517434/17028705 | 0.500180959151033504896584913532 | 1.198363 |
| 29 | 2 | 912105/1823671 | 912105/1823671 | 0.500147778848268136083756335435 | 1.202325 |
| 30 | 118 | 54475104/108923721 | 18158368/36307907 | 0.500121585086135645329266707662 | 1.191526 |
Dans le cas particulier du mot de Kolakoski, on peut obtenir d’encore meilleurs bornes; sachant que le mot est un chemin infini partant de l’état 1…1, il suffit de regarder uniquement la composante connexe de Tn * W3 contenant cet état.
| n | nbr. arcs | cycle moyen max. | fraction réduite | forme décimale |
| 4 | 1 | 22/42 | 11/21 | 0.523809523809523809523809523809 |
| 5 | 2 | 36/69 | 12/23 | 0.521739130434782608695652173913 |
| 6 | 2 | 64/123 | 64/123 | 0.520325203252032520325203252032 |
| 7 | 2 | 64/123 | 64/123 | 0.520325203252032520325203252032 |
| 8 | 4 | 286/561 | 26/51 | 0.509803921568627450980392156862 |
| 9 | 4 | 286/561 | 26/51 | 0.509803921568627450980392156862 |
| 10 | 4 | 369/729 | 41/81 | 0.506172839506172839506172839506 |
| 11 | 8 | 1432/2835 | 1432/2835 | 0.505114638447971781305114638447 |
| 12 | 2 | 694/1377 | 694/1377 | 0.503994190268700072621641249092 |
| 13 | 4 | 1926/3827 | 1926/3827 | 0.503266266004703423046772929187 |
| 14 | 10 | 7999/15913 | 7999/15913 | 0.502670772324514547853955885125 |
| 15 | 20 | 21182/42171 | 21182/42171 | 0.502288302387896895971165018614 |
| 16 | 3 | 5358/10669 | 114/227 | 0.502202643171806167400881057268 |
| 17 | 4 | 10572/21076 | 2643/5269 | 0.501613209337635224900360599734 |
| 18 | 30 | 121359/242103 | 40453/80701 | 0.501270120568518357888997658021 |
| 19 | 15 | 66312/132349 | 66312/132349 | 0.501038919825612584908083929610 |
| 20 | 62 | 483437/965252 | 483437/965252 | 0.500840195099310853538765006443 |
| 21 | 44 | 544089/1086621 | 181363/362207 | 0.500716441151054507505376759698 |
| 22 | 62 | 1083479/2164455 | 1083479/2164455 | 0.500578205599100004389095638393 |
| 23 | 30 | 813542/1625534 | 406771/812767 | 0.500476766404147806197840217430 |
| 24 | 87 | 3779734/7553622 | 1889867/3776811 | 0.500386966676383859292932582541 |
| 25 | 73 | 4969453/9932530 | 4969453/9932530 | 0.500320965554596865048482108787 |
| 26 | 54 | 5434523/10863243 | 5434523/10863243 | 0.500267093353246355623270141338 |
| 27 | 4 | 355310/710263 | 355310/710263 | 0.500251315357832239607018808525 |
| 28 | 26 | 5543742/11083545 | 1847914/3694515 | 0.500177695854530296940193773742 |
| 29 | 43 | 14008501/28008925 | 14008501/28008925 | 0.500144186183511148678501584762 |
| 30 | 5 | 2734171/5467038 | 2734171/5467038 | 0.500119260191716245615999010798 |
Soit C∞ l’ensemble des mots lisses finis. Soit 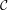 (C∞) l’ensemble des mots lisses
bi-infinis.
(C∞) l’ensemble des mots lisses
bi-infinis.
Les codes préfixes, suffixes, bifixes (maximaux ou non) de C∞ sont définis naturellement. (Ensembles finis ou non de mots finis dans C∞).
Exemple. Les codes suivants sont des codes bifixes maximaux de C∞: {1,2}, {11,12,21,22}, {112,121,122,211,212,221}, {11,121121,12112212,1212,1221,2112,2121,21221121,212212,22}.
Question. Existe t’il un code bifixe de C∞ infini ?
Remarque. Il y a un papier[] sur les codes bifixes dans les langages factoriels récurrents (a.k.a. transitifs). Beaucoup des conjectures qui suivent sont démontrés dans ce cas. Les mots lisses sont factoriels, mais ne sont pas démontrés être récurrents (il s’agit de l’Universal Glueing Conjecture[]).
Soit f : C∞→ ℝ+ la mesure de Dekking. On voit directement que :
Proposition. Soit X un code préfixe maximal. Alors ∑ w∈Xf(w) = 1.
Soit X un code. Soit d(X) = ∑ w∈X|w|f(w).
Conjecture. Soit X un code bifixe maximal de C∞. Si d(X) est fini, alors d(X) est un entier.
Question. Existe t’il un code bifixe de C∞ avec d(X) = ∞ ?
Conjecture. Soit X un code bifixe maximal de C∞. Il existe un d′(X) ∈
ℕ+ ∪{∞} tel que pour tout w ∈ 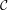 (C∞), il y a exactement d′(X) façons de
décomposer w avec X.
(C∞), il y a exactement d′(X) façons de
décomposer w avec X.
Conjecture. Soit X un code bifixe maximal de C∞. Alors d(X) = d′(X) (le degré de X).
Observation. Les mots de retour valides pour un état v dans Tn sont des codes bifixes maximaux. Les mots de retour valides dans Tn sont des codes bifixes maximaux.
(note: les mots de retour de taille 0 modk sont aussi des codes bifixes, mais on a plus forcement un degré 2x.)
Les codes de retour de T, T2 et T3 sont respectivement W1, W2 et W3, et sont respectivement de degrés 2, 4 et 8. Les codes de retour des état de T (resp. T2, T3) sont tous les mêmes, et tous égaux à W1 (resp. W2, W3). Ceci n’est plus vrai pour T4. Le code de retour de T4 est de degré 32, et est de taille 2810, tandis qu’il y a deux codes de retours différents pour les états de T4, tous deux de degré 16 et de taille 228. Le code de retour de T5 est de degré 256, et est de taille 720074. Il y a quatre codes de retours différents pour les états de T5, tous de degré 32, et de taille 1678 ou 1768.
Le code de retour vers un état v1 (resp. v2) dans Tn+1 est construit depuis le code de retour vers v dans Tn avec l’opération suivante.
Conjecture. L’opération précédente double le degré de W, pour tout code bifixe maximal W.
Idée de preuve (si on construit W′à partir de W): on regarde W′ comme des mots sur l’alphabet W. Pour w ∈ W, soit g(w) = ∑ w′∈W′|w′|wf(w′). Il faut montrer que g(w) = 2 pour tout w ∈ W (ce qui montre la conjecture). Le degré du code bifixe W′ sur l’alphabet W est de 2, car il existe deux parses possibles (car il y a 2 états possibles). Mais l’égalité average length = nombre de parses n’est pas prouvé, car on a pas la récurrence pour pouvoir appliqué les résultats connus.
(C’est peut être plus facile à voir avec les mots de retour dans les transducteurs qu’avec la définition directe.)
Si on montre qu’un code bifixe de degré fini est fini, on montre que tout chemin infini valide dans un Tn est uniformément récurent. (Mais je ne n’ai pas d’intuition sur le fait que tout code de degré fini est fini.)
Si on montre que tous les mots de retours sont finis, on montre la récurrence du mot de Kolakosi. Soit v un facteur f apparaissant dans κ. Soit n tel que v apparaisse dans un. κ sera induit par une suite infinie de chemins de retour dans Tn. Donc v apparaîtra (au moins) à chaque re-passage à o.
Question. Existe t’il, pour tout k > 0, un mot wk ∈ C∞ tel que pour tout 0 ≤ l ≤ k, Δl(wk) est pair ?
À vérifier: soit w un mot de retour dans Tk+1. Alors Fk(w) répond à la question précédente. Montrer que le code bifixe de retour d’un Tn est de degré 2n répond par l’affirmative à la question précédente pour tout k.
L’utilisation de Tn peut servir à avancer rapidement dans la génération du mot.
Voici le nombre de 1 dans les 10x premières lettres de κ (séquence A195206 de l’OEIS).
| 100 | 1 |
| 101 | 5 |
| 102 | 49 |
| 103 | 502 |
| 104 | 4996 |
| 105 | 49972 |
| 106 | 499986 |
| 107 | 5000046 |
| 108 | 50000675 |
| 109 | 500001223 |
| 1010 | 4999997671 |
| 1011 | 50000001587 |
| 1012 | 500000050701 |
| 1013 | 5000000008159 |
| 1014 | 50000000316237 |
| 1015 | 500000000977421 |
| 1016 | 4999999994637728 |
| 1017 | 49999999977479348 |
| 1018 | 499999999944465105 |
Plus de valeurs ici. Si vous voulez encore plus de valeurs, essayez le Kolakotor (si l’ordinateur maître est disponible).
Les graphes des différences jusqu’à 10x, 3 ≤ x ≤ 18 ici.
Un mot w est lisse (smooth) si pour tout k ∈ ℕ, δk(w) est dérivable. Soit C∞ l’ensemble des mots lisses.
Soit f(n) = maxw∈C∞:|w|=n|w|1.
A. Carpi conjecture[2] que f(n) - n∕2 = O(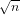 ).
).
Voici les valeurs de 2 ⋅ f(n) - n pour 0 < n ≤ 66704 : 66704.txt.
[1] Srecko Brlek, The last talk on the Kolakoski sequence, BIRS workshop “Outstanding Challenges in Combinatorics on Words” (Février 2012).
[2] Arturo Carpi, On repeated factors in C∞-words, Information Processing Letters Vol 52(6) (1994) 289–294.
[3] Vašek Chvátal, Notes on the Kolakoski Sequence, DIMACS Technical Report (1993), 93-84.